Bayangkan Anda diminta untuk menghitung ubin yang diperlukan untuk menutupi permukaan lantai aula suatu sekolah menengah atas (SMA). Setelah melakukan investigasi ringan, Anda tahu bahwa ruangan tersebut berukuran 15m x 40m. Untuk mempermudah perhitungan, Anda pun bisa berasumsi boleh menggunakan satu jenis ukuran ubin kesukaan Anda, yakni Supermilan ukuran 50cm x 50 cm. Maka berapakah jadinya ubin yang diperlukan untuk menutup semua permukaan aula SMA tersebut?
Sangat mudah. (15m/50cm) x (40m/50cm) = 30 x 80 = 2.400 ubin. Jika pengen tahu berapa dos (kardus) yang diperlukan, tinggal dibagi 4, karena ada 4 ubin 50cmx50cm per kardusnya. Dengan demikian dibutuhkan 600 kardus.

Gampang. Tidak ada yang spesial.
Sekarang mari kita lompat ke level yang baru. Anda seolah-olah adalah Mario Bellini, yang ditugasi untuk mengarsiteki The Cour Visconti di Museum Louvre yang tersohor di Perancis itu. The Cour Visconti merupakan ‘karpet terbang’ yang menjadi atap bagi ekshibisi kesenian Islam di salah satu bagian Museum Louvre.
Tugas Anda: merancang permukaan atap agar berbentuk seperti karpet terbang (salah satu dari jenis free-form surface) yang bergelombang dengan indah, di sisi lain, permukaan itu pun harus bisa ditutupi dengan struktur yang sederhana dan berpermukaan datar. Ada satu bagian yang mirip dengan kasus ubin tadi: Anda perlu menentukan bentuk dasar ‘ubin’-nya (bisa berupa segitiga, persegi, persegi panjang, jajar gendang, dll) lalu menghitung berapa ubin yang diperlukan. Silakan lihat gambar pada slideshow [1] di bawah sebagai acuan.
Kini kasusnya menjadi semakin menarik. Lebih susah.
- Bentuk secara umum dari si karpet terbang The Cour Visconti adalah bergelombang (bahasa ilmiahnya dia merupakan salah satu bentuk free form surface) tetapi bentuk dasar yang bisa digunakan sebagai ‘ubin’ punya permukaan datar
- Tidak ada ketentuan pasti berapa ukuran ubin/genteng yang diperbolehkan, tetapi mereka harus punya ukuran yang hampir seragam. Tantangan kita untuk menghitung ukuran ubin, lalu kemudian jumlahnya.
- Akan sangat jelek jika di bagian tepi/pojokan/tengah ada bagian yang perlu dipotong karena terlalu panjang atau lebar ukurannya.
Lalu bagaimana kita mengerjakannya?

Untuk menyelesaikan permasalahan di atas, upaya coba-coba, bongkar-pasang akan menjadi sangat mahal, baik secara waktu maupun tenaga dan pikiran, juga biaya. Diperlukan proses automasi–dengan bantuan komputer–supaya problem bisa diatasi dengan baik: akurat dan lebih hemat sumber daya.
Di bagian inilah geometry modeling and processing mempunyai kontribusi pentingnya.
Secara garis besar, Mario Botsch dkk menjelaskan dalam bukunya Polygon Mesh Processing bahwa geometry processing [2] merupakan bidang dalam ilmu komputer yang berkaitan dengan model matematis dan algoritme untuk menganalisis dan merekayasa (mengolah) data geometris. Bidang ini mempunyai peran untuk memperoleh, menganlisi, dan merekaya model geometri dari suatu objek 3 dimensi [3]. Banyak peneliti memberikan karya-karya terbaiknya agar proses automasi bisa dikerjakan secara lebih baik.
Sebelum kita bisa membagi area karpet terbang menjadi banyak bagian kecil ubin, kita pertama-tama harus memodelkan bentuk geometri dari karpet terbang tersebut. Karena kita perlu mewujudkannya dalam bentuk fisik, maka salah satu cara paling bagus adalah dengan membuatnya dalam model developable surface [4], yakni permukaan dengan nilai kurvatur Gaussian 0. Kita bisa menggunakan Bezier Surface [5] sebagai elemen dasarnya.
Teknik pemodelan ini bisa sangat bervariasi, menyesuaikan kebutuhan dan kondisi kita. Bisa membuat sendiri jika mampu atau menggunakan tools yang telah ada. Salah satu perangkat lunak yang banyak digunakan adalah AutoCAD untuk mendesain berbagai bangunan dan bagian bangunan. Berbagai algoritme geometry processing telah diselipkan ke dalam perangkat lunak buatan Autodesk tersebut, sehingga desainer atau arsitek bisa lebih mudah dalam merealisasikan mimpinya. Sebagai contoh, dengan fitur PressPull di AutoCAD [6], desainer bisa merancang lantai bangunan dengan berbagai bentuk unik dari kurva bebas (NURBS/B-Spline) dan tinggal menariknya ke atas sehingga keseluruhan bangunan akan benatuk yang sama dengan dasaran/alasnya.
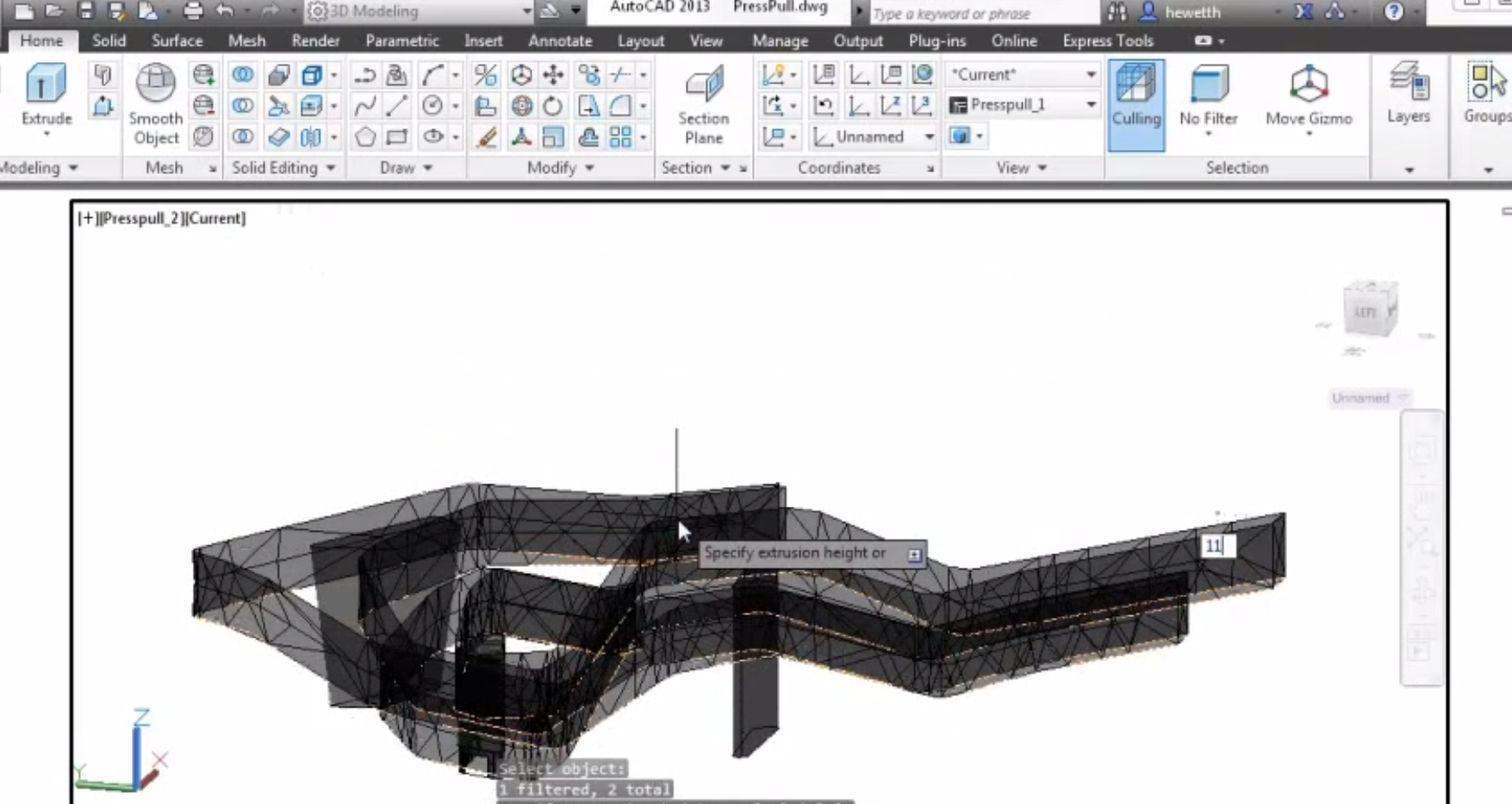
Dengan perangkat lunak pemodelan saja proses ini belum berakhir, masih ada proses manufaktur/produksi untuk mewujudkan desain ke dalam bentuk nyata. Bagaimana caranya memotong bagian yang besar dari free form surface (misal: karpet terbang) menjadi bagian kecil-kecil yang memungkinkan secara fisik untuk diproduksi dengan biaya seefisien mungkin [7]. Proses ini sering disebut rationalization dalam bahasa geometry processing, karena bidang ini masih baru, caranya tentunya sangat bervariasi, berlomba-lomba menghasilkan luaran terbaik untuk panelisasinya.
Angka dari jumlah panel/ubin untuk The Cour Visconti memang tidak terjawab dari artikel singkat ini, tetapi saya berharap kita semakin terbuka akan perlunya dan pentingya Geometry Processing dalam berbagai sisi kehidupan kita, dalam membantu manusia mengatasi berbagai masalah yang dihadapinya.
Referensi:
- Gambar dari http://www.dezeen.com/2012/09/24/department-of-islamic-arts-at-louvre-by-mario-bellini-and-rudy-ricciotti/
- Botsch, M., Kobbelt, L., Pauly, M., Alliez, P., & Lévy, B. (2010). Polygon mesh processing. CRC press.
- Ben Chen, M .Geometry Processing Algorithms. Computer Graphics, Stanford University. http://graphics.stanford.edu/courses/cs468-12-spring.
- Developable Surface. https://en.wikipedia.org/wiki/Developable_surface
- Bezier Surface. http://homepages.inf.ed.ac.uk/rbf/CVonline/LOCAL_COPIES/AV0405/DONAVANIK/bezier.html.
- Context-Sensitive PressPull Tool. http://www.autodesk.com/products/autocad/features/innovative/context-sensitive-presspull-tool
- Pottmann, H., Eigensatz, M., Vaxman, A., & Wallner, J. (2015). Architectural geometry. Computers & graphics, 47, 145-164.