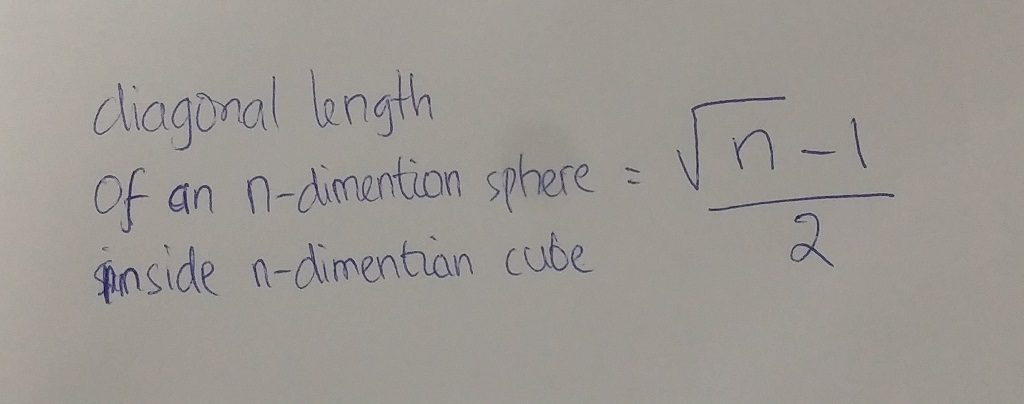Berawal dari keisengan browsing video di Youtube, saya terjebak dalam ketertarikan pada ‘dimensi tinggi’ (Higher Dimension). Bukan ketertarikan akademis/profesional yang membutuhkan kepakaran ilmu, tetapi sekedar hobi, hal-hal yang dilakukan saat waktu senggang. Adalah salah satu video awal dalam kelas Topology & Geometry yang diadakan oleh African Institute for Mathematical Sciences yang memberikan gambaran tentang fenomena menarik ini: bahwa benda yang berada dalam benda lain (sama-sama solid/padat) bisa berukuran lebih besar dari benda yang ada di luar.
Untuk memulai, mari kita mengawali dengan konfigurasi seperti ini: kita punya persegi (kubus 2 dimensi) dengan panjang sisi-nya 1 unit satuan; persegi tersebut kita bagi menjadi 4 persegi yang lebih kecil dengan ukuran yang sama luasnya sehingga masing-masing punya sisi 0.5 unit satuan; di dalam tiap persegi kita gambar lingkaran dengan diameter 0.5 unit satuan (jari-jari 0.25) sehingga menempel pada sisi keempat persegi tadi.
Pertanyaannya: Jika kita menggambar 1 lingkaran kecil, dengan pusat lingkaran berada pada pusat persegi, sehingga lingkaran itu bersentuhan dengan lingkaran-lingkaran di luarnya, berapa diameter dari lingkaran kecil tersebut?
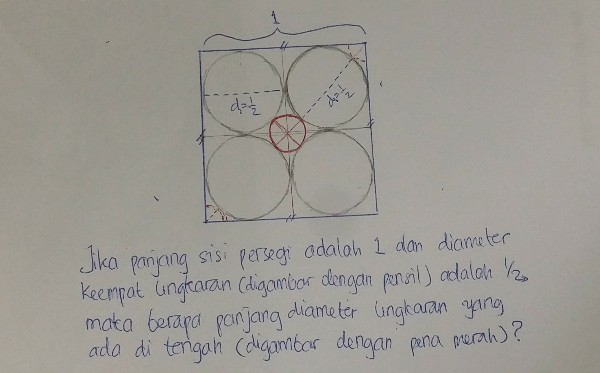
Dengan menggunakan analisis Geometri sederhana, kita bisa menghitung jari-jarinya, yaitu setengah dari akar dua dikurangi satu. Perhitungannya seperti gambar berikut ini.

Kubus 3 Dimensi
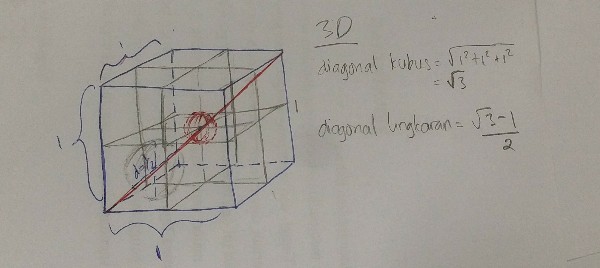
Nah, sekarang mari kita lakukan hal yang sama pada kubus, benda 3 dimensi. Kita buat satu kubus dengan rusuk-nya masing-masing punya 1 unit satuan panjang. Kemudian kita bagi menjadi 8 bagian kubus dengan rusuk 0.5 unit satuan yang mana di dalamnya kita buat 1 bola (sphere) dengan diamater 0.5 unit satuan. Di tengah-tengah kedelapan bola tersebut, kita buat bola lebih kecil yang menyentuh kedelapan bola yang lebih besar tadi.
Masih dengan pertanyaan yang sama: Berapa panjang diameter bola kecil tersebut?
Kubus N Dimensi
Bagaimana jika hal yang sama kita lakukan pada tesseract (kubus 4 dimensi) atau kubus-kubus pada dimensi yang lebih tinggi? Berapa diameter bola N dimensi yang berada pada kubus N dimensi tersebut?
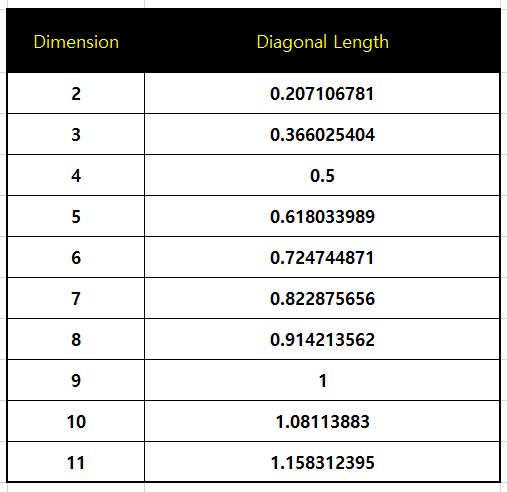
Secara sekilas kita bisa amati bahwa panjang diagonal kubus N dimensi adalah akar dari (1 kuadrat + 1 kuadrat + … sebanyak n kali) yang itu bernilai akar(N). Dari satu ujung kubus N dimensi ke ujung lainnya, kita hanya akan melewati dua bola N dimensi, yang mana masing-masing diameternya adalah 0.5 unit satuan. Karena panjang diagonal pada kubus N dimensi adalah akar(N), lalu total diameter dari bola N dimensi adalah 1 unit satuan (0.5 + 0.5), serta ada dua bola N dimensi yang berada pada 1 diagonal tersebut, maka panjang diameter lingkaran tengah pada N dimensi kubus adalah:
Lalu apa yang menarik? Jika kita amati sekilas, panjang diameter sangat bergantung pada dimensi kubus (N). Semakin tinggi dimensinya maka semakin panjang pula diagonal pada kubus N dimensi, yang berimplikasi semakin panjang pula diameter bola N dimensi yang berada pada kubus N dimensi tersebut. Pada saat kita memasuki dimensi >9, maka panjang diagonal dari bola N dimensi yang berada di dalam kubus N dimensi (dan sejumlah 2^n bola N dimensi dengan diameter 0.5 unit satuan) lebih besar dari panjang sisi dari kubus (1 unit satuan). Dengan kata lain, bola N dimensi tersebut berukuran lebih besar dibandingkan dengan kubus N dimensi yang berada di luarnya (dalam hal diameter).
Benda-benda dalam dimensi tinggi memiliki karakter yang berbeda dengan dunia 3 dimensi kita. Kita pun perlu menyesuaikan pola pikir kita agar bisa memahami karakter dari ruang dengan dimensi yangl lebih tinggi. Dengan memahami itu, kita akan terbuka pada bentuk ‘keindahan’ di luar sana yang kita belum pernah bayangkan atau ketahui.