[PEMODELAN GEOMETRI]
Seandainya kita iseng mencolokkan jarum panas ke tengah gigi kawan kita, bagaimana ya kira-kira perseberan panas yang disebabkan oleh jarum itu pada permukaan gigi kawan kita? Seandainya kita punya miniatur Centaurus dan kita ingin menempelkan selotik dari ujung kepala hingga pangkal ekornya, berapa panjang ya selotip yang kita butuhkan?
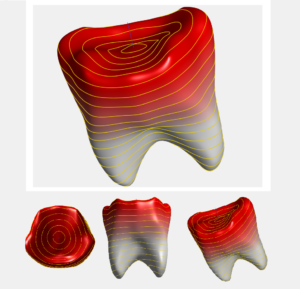
Dalam bidang keteknikan, ada satu topik yang sering digunakan, yaitu heat transfer (perpindahan panas). Dalam bidang kami (geometry processing), perpindahan panas secara difusi pada permukaan bidang/objek bisa digunakan untuk mengukur jarak para bidang/permukaan objek tersebut [1].
Salah satu teknik yang relatif banyak digunakan untuk mengukur jarak di permukaan model dengan menggunakan difusi panas adalah Heat Method [2]. Secara umum, teknik ini merupakan persamaan diferential (PDE) yang mana perubahan panas di satu titik persatuan waktu berbanding lurus dengan percepatan perubahan panas ((positive/negative) semidefinite Laplace-Beltrami operator, jika hendak pengen lebih tekniks^^). Kemudian berdasarkan gradient (turunan pertama pada multi-variable calculus) kita bisa menghasilkan vector field yang menunjukkan arah persebaran panas. Terakhir, dengan ada persamaan Poisson yg bisa diselesaikan oleh Matlab/solver lain, cukup kita masukkan saja rumus dan angka-angkanya.
Secara umum, ada tiga langkah untuk mengimplementasikan Heat Method, sebagaimana dijelaskan oleh Crane di artikelnya [2]. Ketiga langkahnya adala sebagai berikut:
- evaluasi nilai integral dari aliran panas du/dt = lambda(u), dengan lambda(u) merupakan matrix Laplace-Beltrami Operator (negative semi-definite) yang dihasilkan dari representasi 3D objek yang hendak kita evaluasi. Langkah untuk menyusun matriks Laplace-Beltrami bisa dilihat di [3].
- dari nilai u yang kita peroleh dari langkah (1) di atas, kita bisa menghitung vector field X dengan formula X=-grad(u).
- selesaikan persamaan untuk psi => Laplace(u) * psi = gradient(u) * X.
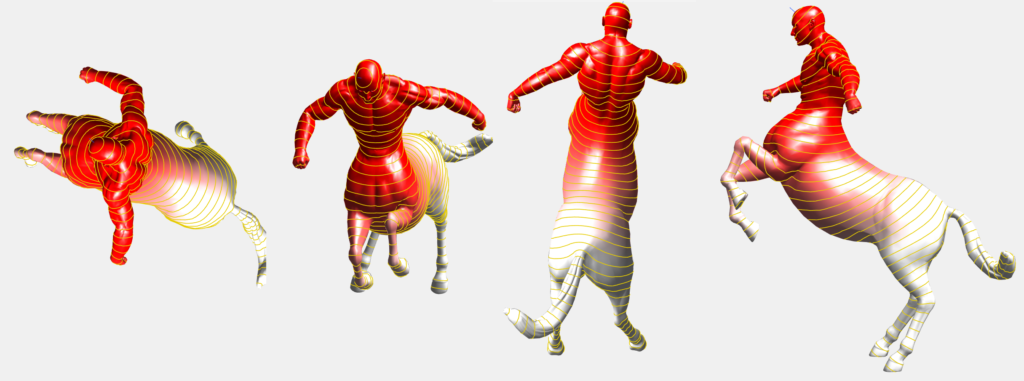
Ada banyak cara untuk mengukur jarak antara dua titik di permukaan model. Yang paling sederhana adalah jarak Euclidean, yakni kita cukup menarik garis lurus antara dua titik itu lalu menghitung jaraknya. Cara yang kedua adalah jarak geodesi, yang mana kita berupaya untuk mengukur jarak di permukaan objek tersebut. Sebagai contoh, Euclidean distance antara jari tengah dan jari telunjuk saat kita membuat tanda “peace” mungkin hanya sekitar 5cm, sedangkan geodesic distance-nya bisa sekitar 12cm. Dalam banyak kasus, geodesic distance biasanya lebih dibutuhkan karena lebih akurat untuk merepresentasikan jarak pada objek, walau komputasinya tentunya lebih rumit. Heat Method ini merupakan salah satu cara untuk menghasilkan jarak geodesi.
Dengan Heat Method ini kita bisa mengkaitkan fenomena perpindahan panas dengan pengukuran jarak geodesi pada suatu objek.
[1] Varadhan, S. R. S. (1967). On the behavior of the fundamental solution of the heat equation with variable coefficients. Communications on Pure and Applied Mathematics, 20(2), 431-455.
[2] Crane, K., Weischedel, C., & Wardetzky, M. (2013). Geodesics in heat: A new approach to computing distance based on heat flow. ACM Transactions on Graphics (TOG), 32(5), 152.
[3] Reuter, M., Wolter, F. E., & Peinecke, N. (2006). Laplace–Beltrami spectra as ‘Shape-DNA’of surfaces and solids. Computer-Aided Design, 38(4), 342-366.